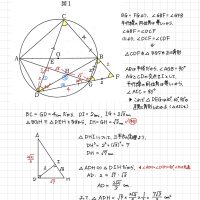
入試問題、最初から問題が分かっていれば解けるのに。
「ねえ、ドラえもん」と、お願いして未来に行って見てくることはできません。
じゃあ、予想して当てちゃいましょう。
こんにちは、予想屋の山田です。
ロト(宝くじ)や競馬など、ちまたではＡＩの予想が流行っていますが、ＡＩに負けないように予想してみたいと思います。

令和２年度 神奈川県公立高等学校入学者選抜学力検査問題(予想問題)

さすがに数学の全問を予想するのは、膨大な時間がかかりますので、問１と問２の計算問題について、予想してみたいと思います。
まず、いきなりですが、予想した問題は下記になります。
＊解答は、来週アップします。
数学予想問題
簡単ですね。
ただ、これは『解ける』じゃダメですよ。
２週間前のブログ『誰でもできる神奈川県公立高校入試対策数学編』でも書いたように、これを『３分』で解くのです。
もちろんミスしないように。
それから１つ補足ですが、問１も問２も、『１～４の中から１つ選び、･･･』となっていますが、これは、実際の入試問題と同じスタイルで表記したかったからです。

ちなみに、過去の入試問題は下記になります。
2019年度(平成31年度・令和元年度)
2018年度(平成30年度)
2017年度(平成29年度)
2016～2012年度
2011～2007年度
2006～2002年度

令和２年度 公立入試 数学の問１

問１(ｱ)の予想コンセプト

３年連続(－○)＋(－△)という出題なので、さすがに次はこの形では出題してこないだろう。

カッコをまったく使わない出題なら、負の数どうしの足し算はないと思う。
何故なら、それでは形が変わったと言っても、計算の本質が４年連続で同じになるからだ。
そうなると、カッコを使わないでの出題なら、当然16年や14年、12年、08年、04年、02年のような異符号の加法だろう。
カッコを使わず正の数どうしの加法では、小学校低学年の計算になってしまう。

では、カッコを１つ使った問題だとしたらどうだろうか。
１つしか使わないとなると、意味のある使い方は13年や11年、09年、07年、05年のような〇－(－△)の形だろう。
この２つのタイプのうち、４択の答えを用意しやすいのは後者と考え、令和２年度入試数学の問１(ｱ)の本命は、この形で出題されると予想する。

使われる数字だが、この18年間ではほとんどが１桁の数である。
前の数と後ろの数、合計で36個(同じ数も含む)もある中で、２桁の数はたった４回だけだ。
そうなると、やはり１桁の数どうしの計算が出題される可能性が高いのかと思われる。
意味がありそうな組み合わせとしては、８－(－６)や７－(－５)のように、正しく計算をすると、くり上がりがあり、間違った計算をするとただの１桁の引き算といったものだろうか。
しかし、４択になった今、くり上がりでの計算ミスを誘うということも不可能なので、違う視点で考えたい。

１桁の数でのやりくりも、もう限界になりつつあるので、今後はもう少し大きな数が頻繁に登場するのではないかと思う。
そう考え、２桁の数のうち過去に登場したことのある２種類の数字の１つ『11』を選んでみた。
いの一番の問題、ここで数学が苦手な生徒に精神的なダメージは与えられないので、突然これまでからは考えられないような大きな数字が出ることはないだろう。

問１(ｲ)の予想コンセプト

こちらも、４択になったことで、これまでの出題形式から変更になる可能性があるような気がする。
しかし、そうは言っても問１の(ｲ)、ここは数学が苦手な生徒にも点数をあげようと考えているはずなので、まだ変更しないという前提での予想。

分母に使われる２つ数字、これらは基本的に互いに素である数字が使われている。
つまり、通分する際、何が最小公倍数なのかを考えなくていいということだ。
何も考えず、分母の数どうしをかければ終了。
そして、答えの符号、ここは『負』になる可能性が８割と予想する。
理由は、そのような調整をしないと、やはりただの小学生の分数計算になってしまうからだ。

問１(ｳ)の予想コンセプト

まず係数について。
この18年間、割り切れる数字しか使われていない。
(ｲ)同様に、４択になったことで今後の変化の可能性はあるが、ここもまだ今まで通りと予想する。

文字についても、答えが分数になることは、これまでの18年間で１度もない。
４択になってまだ２回しか問題を見ていないので、出題者が用意する答えの方向性が分からないが、18年と同じようなミスを誘う答えを用意すると予想し、係数は36と６のような組み合わせと結論。
18年と同じミスを誘うということで、当然、選択肢には『６』と『３』が用意されているという予想である。
ちなみに、ここも答えの符号は『負』の可能性が高いと判断し、36とー６という数字にした。

問１(ｴ)の予想コンセプト

根号を含む加減で出題者が確認したい知識は、もちろん『有理化』。
つまり、前か後かどちらかには、必ず『ルート何とか分の整数』という数が出てくるはず。
そして、この１問で分数の計算力までは問わないはずなので、その数は有理化したらほぼ間違えなく分数の形ではなくなるはずと予想。

分母のルートの中の数字は１桁。
そうなると、可能性のある数字は２、３、５、６、７、８。
しかし、８はａ√ｂの形に変形できる数字なので、まず使われない。
したがって、２、３、５、６、７のどれかが使われるはずである。
７は19年(前年)に使われた数字。
２は直近の５年間で２度使われている数字。
５は、倍数の判定が簡単なので、あまり(私自身が)使いたくない数字。
残った数字は３と６。
(ｳ)で６がらみの問題を予想したので、ここで使われる数字は『３』と結論。

問１(ｵ)の予想コンセプト

ここは、まず間違えなく(　)(　)－(　)２か(　)２－(　)(　)の２択。
ようは、正しく－の処理をできているかどうかということ。

これを確認したいなら、正しく計算(－の処理)ができていれば、１次の項が消えるような問題にするのが一番分かりやすい。
数学が苦手な生徒は、項が消えることに不安を持っている。
例えば、４ｘ－３ｘの答えを自信を持ってｘと書くのに、４ｘ－４ｘの答えも何故かｘと書く。
直近の10年では、前者のタイプが４回、後者のタイプが６回、次は前者のタイプと予想。

令和２年度 公立入試 数学の問２

問２(ｱ)の予想コンセプト

ここでやらせたいのは『置き換え』による計算。

もちろん、置き換えをしなくても解けるが、置き換えをしないで計算すると途中の計算が大変になるような数字にしてくるはず。
置き換えをしなかった場合に計算が大変になるような調整としては、置き換え部分の数値を大きくするのではく、第２項の係数を７としたように、ここの数字を大きな数にしてくるのではないかと予想。
問２の(ｱ)は、最初から置き換えをするんだという目線で問題を見るべし。
置き換えさえしてしまえば、あとは簡単な因数分解になるはず。

問２(ｲ)の予想コンセプト

ここで確認したい知識は、99％『解の公式』以外ないはず。

もし文章問題で２次方程式が出題されたなら、その式は因数分解で解ける式になるはず。
２次方程式の解き方の中で平方完成があるが、１度の入試問題という限られた中では、それを問う問題をピンポイントで出題するのは難しいと考える。
したがって、この２次方程式の問題で問うのは、『解の公式』が99％と結論。

あとは、係数がどうなるか。
そこで言えるのは、私が出題者なら、１次の項の係数を『負の偶数』にするということだ。
理由は３点ある。
１つは、負の数にすることによって、分子の『－ｂ』での代入ミス、これが上がる。

２つ目は、偶数にすることによって、必ず約分が発生するということである。
解の公式には、偶数バージョンもあるが、それは中学の学習指導要領外である。
塾などでは教える場合があるが、基本はそれを知らないので、正しく約分ができるかどうかの確認ができる。

３つ目、これは、係数ａを１にすれば、平方完成と両天秤にかけることができるからだ。
係数ａが１でｂが偶数の場合、平方完成を使える生徒は、その解き方の方が計算が簡単になる。
つまり、仮に解の公式で解かなくても、平方完成の知識を確認することができる。
多くの中学生の立場からすると、平方完成と解の公式では、解の公式の方が使いやすいと感じている。
感じているというより、そのような生徒は、きっと平方完成はできない。
その２つの解き方の中で、あえて平方完成を選んでその解き方で解いているなら、その生徒は間違えなく解の公式も使いこなせる。

連立方程式について

ちなみに、ここ最近では計算問題として連立方程式が出題されていない。
昔は、問１や問２の計算問題で出題される可能性があった連立方程式だが、これは、今後も出題されないと予想する。
何故なら、連立方程式の知識は、他の問題で確認することができるからだ。

関数の問題、これがそれだ。
交点の座標を求めよという直球を出題せずとも、(ｳ)を解く過程で交点の座標を求めなければ解けない問題にすればいい。
したがって、コンパクトにまとまった入試問題では、計算問題として連立方程式を出題するのはムダがあると考える。

まとめ

以上が、令和２年度、神奈川県公立高等学校入学者選抜学力検査問題、数学の問１と問２の計算問題の予想です。
さすがに、無限にある数の組み合わせまでドンピシャで当てるのは至難の業ですが、予想コンセプトを参考にしていただければ、効率よく勉強ができるかと思います。

数学が苦手な生徒達、何としても計算問題はパーフェクトでいきましょう。

数学が得意な生徒からすると、計算問題なんて別にどうでもいいよと思ったかもしれません。
ただ、得意な生徒は、ここをスピーディーにかつ正確に通り過ぎなければいけません。
『問１(ｵ)』でのミスしやすいところ、伝えましたので注意して下さい。
また、『問２(ｱ)』と『問２(ｲ)』への取り組み方、時間を１秒でも削りたいので、上記で書いたような視点で見ることで、ノンストップで進めると思います。

では、頑張って下さい。

この記事を書いた人

山田 明史
投稿タグ
, ,